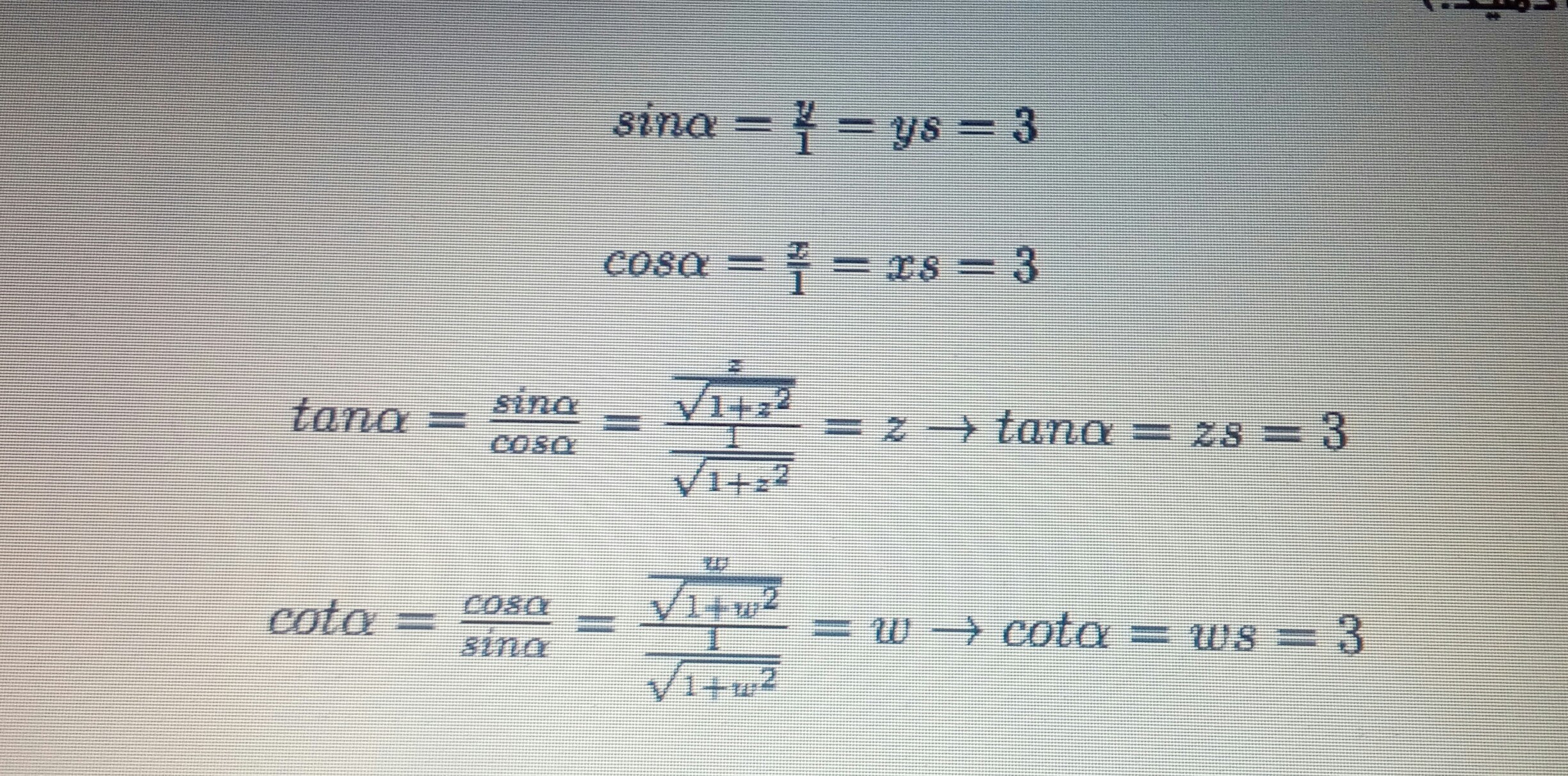دایره مثلثاتی

   

دایره مثلثاتی یکی از بهترین راه‌ها برای درک مفهوم نسبت‌های مثلثاتی و حفظ کردن روابط بین آنهاست. اگر به دایره مثلثاتی و نکات آن مسلط شوید، کارتان در حل معادلات مثلثاتی و تبدیل زوایا بسیار راحت خواهد شد.

دایره مثلثاتی چیست؟

دایره مثلثاتی، دایره‌ای به شعاع یک است که مرکز آن بر روی مرکز محورهای مختصات قرار دارد.

 

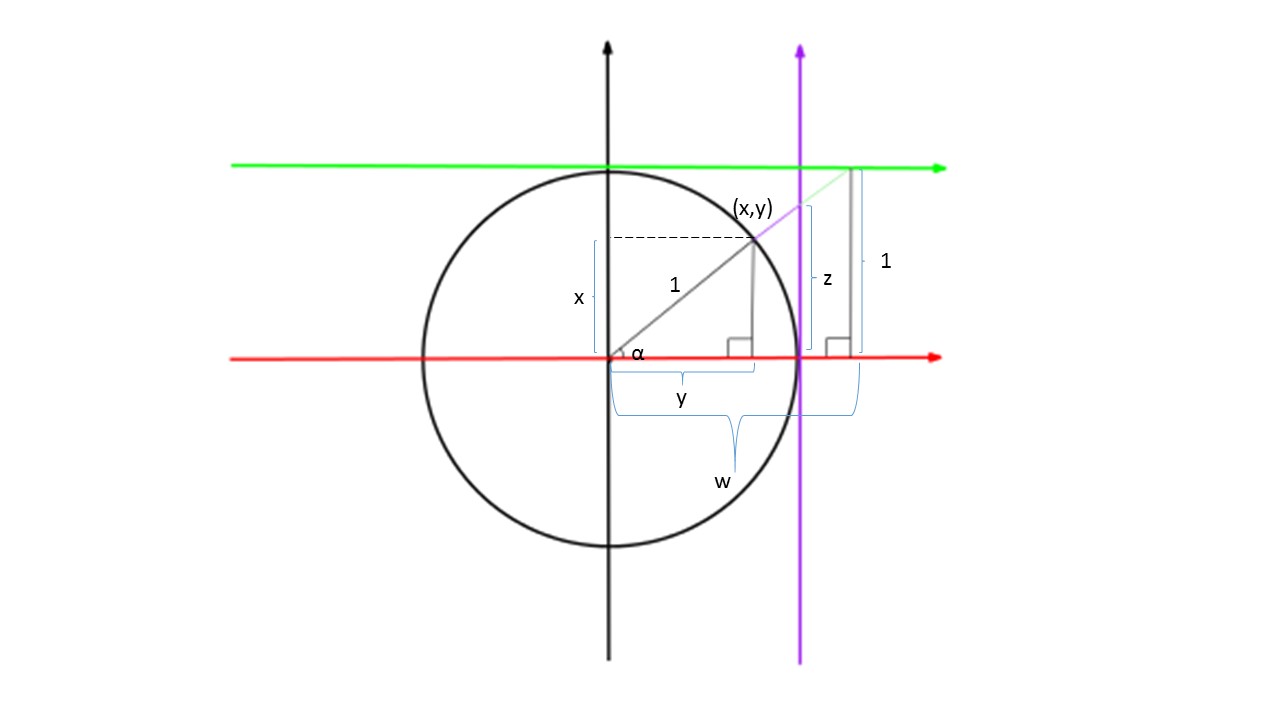
خوب خاصیت این دایره و رابطه آن با نسبت‌های مثلثاتی، چیست؟ بیایید مثل همیشه، یک مثلث قائم‌الزاویه رسم کنیم. زاویه ۹۰ درجه این مثلث بر روی محور xها و یکی از رئوس آن روی محیط دایره واقع شده است.

درست مثل شکل زیر:

حال بیایید، نسبت‌های مثلثاتی را برای زاویه  as = 11 حساب کنیم. (فرمول‌های زیر را با شکل مطابقت دهید.)

همانطور که می‌بینید، مقادیر سینوس روی محور yها، مقادیر کسینوس روی محور xها، مقادیر کتانژانت روی محور عمودی بنفش رنگ (خط x=1) و مقادیر کتانژانت روی محور افقی سبز رنگ نگاشت (خط y=1) می‌شوند.

 

 

تعیین علامت نسبت‌های مثلثاتی روی دایره مثلثاتی

اگر دایره مثلثاتی را در ذهن خود داشته باشید، تعیین علامت نسبت‌های بسیار ساده است.

• علامت سینوس همواره با علامت y برابر است.
• علامت کسینوس همواره با علامت x برابر است.
• اگر امتداد زاویه خط x=1 را در بالای محور xها قطع کرد، علامت تانژانت مثبت و در غیر اینصورت منفی است.
• اگر امتداد زاویه خط y=1 را در سمت راست محور yها قطع کرد، علامت کتانژانت مثبت و در غیر اینصورت منفی است.

 

 

تبدیل زوایا در دایره مثلثاتی

اگر دایره مثلثاتی را حفظ باشید، نوشتن فرمول‌های تبدیل زاویه خیلی راحت می‌شود. به مثال‌های زیر توجه کنید.

• فرض کنید می‌خواهیم رابطه بین نسبت‌های مثلثاتی زاویه  و  را بیابیم.

می‌دانیم که زاویه منفی یعنی حرکت در خلاف جهت عقربه‌های ساعت. پس در خلاف جهت عقربه‌های ساعت به اندازه آلفا پیش می‌رویم. مثلث قائم‌الزاویه‌ای که تشکیل می‌شود، دقیقا مشابه مثلث قبلی است. با این تفاوت که در ربع چهارم است. پس سینوس آن منفی است و کسینوس مثبت. تانژانت و کتانژانت هم منفی می‌شوند.

به همین صورت می‌توانید هر زاویه‌ای را تصور کنید. البته به صورت کلی، قانونی که برای زاویه حاده در ربع اول به دست بیاید، برای تمام زوایا برقرار است.

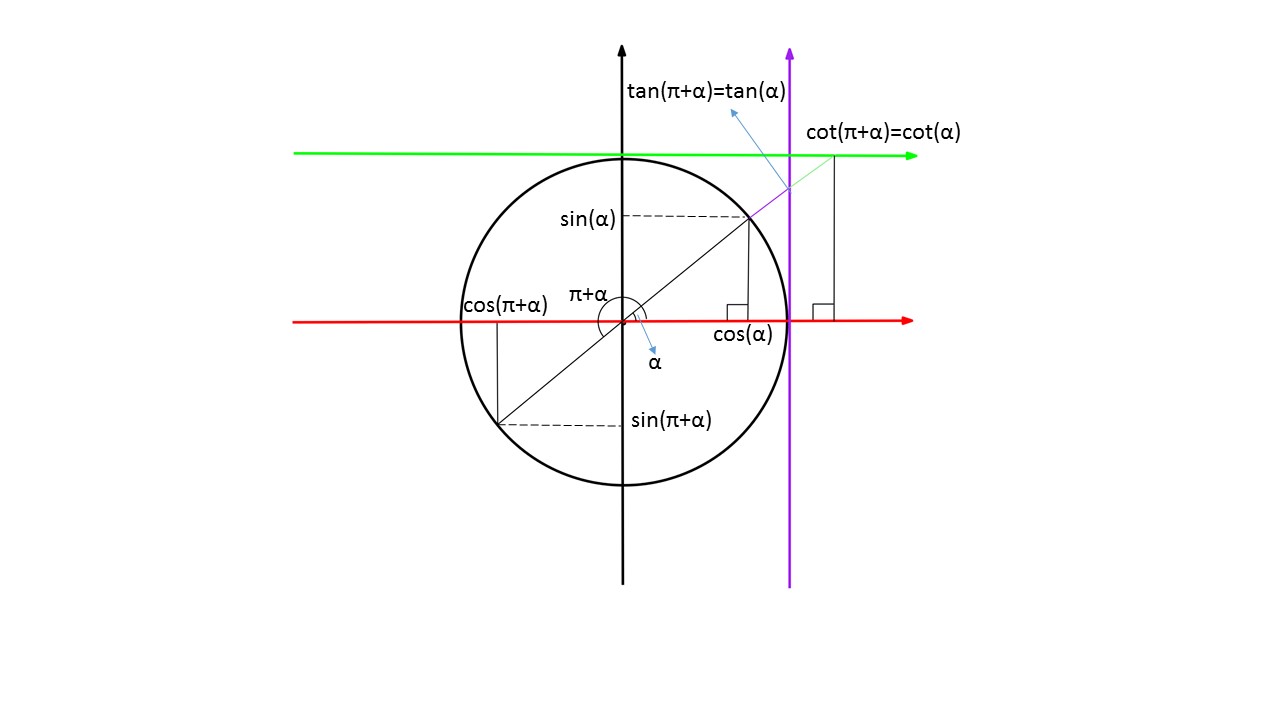
• می‌خواهیم رابطه بین نسبت‌های as=2  و n+as=2 و  n-as=2  را بیابیم.

مطابق مورد قبلی، کافیست که برای یک زاویه حاده، زوایای را تصور کنیم. وقتی زاویه حاده باشد،

n+as=2 و n-as=2 به صورت زیر خواهد بود.

ملاحظه می‌کنید که مثلث‌های قائم‌الزاویه متشابهند. یعنی فقط علامت زوایا عوض می‌شود.